PDF格式（左键浏览，右键另存）：

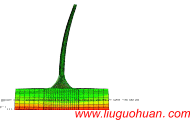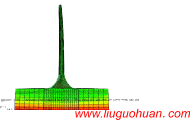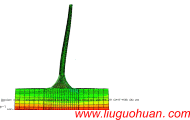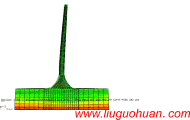
A practical calculating model including multi-mode contributions for along-wind responses of lattice towers

<!--Vol. 6, No. 4 (2012)《Journal of Earthquake and Tsunami》

Abstract：A practical calculating model, based on the fundamental mode generalized force spectrum (FMGFS) obtained in a wind tunnel test and presented practical higher mode generalized force spectrum (HMGFS) model in along-wind direction of lattice tower, is further deduced and proposed to calculate along-wind displacement response of lattice tower. In the proposed model, the contributions of higher vibration modes can be taken into account. As for lattice tower, it is of value to popularize the proposed model and the approach that can provide valuable reference for code.
Keywords：Along-wind-induced dynamic responses;Transmission tower; Generalized force spectrum.

Introduction
Lattice high-rise structure such as transmission tower, with the characters of lightweight, highness,flexibility and low damping, is sensitive to wind load[1]. It is a necessary condition to accurately calculate the wind load before further conducting the structural design. The wind load on structure can be qualified through the multiple-point  synchronous scanning of pressures (MPSSP) on a structure model surface in a wind tunnel, or by a high frequency fore balance (HFFB) measure. Different from the ordinary building, however, the wind load on the transmission tower is difficult to, even can not, be measured in detail using MPSSP measures due to its high hollowness rate, while the HFFB measure is usually used to offer an estimate of the generalized force of the fundamental mode and the FMGFS. Then, according to the random vibration theory, the variance of the responses only including the first mode can be further deduced. However, higher modes may have noticeable contributions to the responses, especially for those slender structures like transmission tower. A systematic work to evaluate along-wind responses of latticed tower was studied by Holmes[2,3,4]. In order to have better understanding of transmission tower-lines system to wind excitation, a novel approach that for the wind tunnel aeroelastic modelling of conductors was introduced in detail by
Loredo-Souza[5,6]. More discussions concerning with the generalized force spectrum of transmission tower have not been addressed. The studies in which three semi-rid tower models were made and HFFB measures were used in TJ-1 boundary layer wind tunnel in Tongji University firstly obtained the FMGFS of transmission tower, and then the HMGFS in an analytic form was also discussed [7]. In order to obtain structural internal force, like the conventional processing approach, the ESWLs only including fundamental modal contribution of transmission tower was also presented [8]. In this paper, for the purpose of practical engineering applications, a practical numerical  MGFS  model is firstly presented on the basis of the fundamental mode generalized force spectrum (FMGFS) obtained from a wind tunnel model experiment and adopting the height-independent fluctuating wind power spectral density and Shiotami-Type spatial coherence function. Then, a practical calculating model for the displacement response is  further deduced. In the formula, the contributions of higher modes can be included and the conversion relations between the unilateral and bilateral power spectral densities are also taken into account in the derivation. er structural design.

Conclusions
According to the analysis above, some conclusions are summarized below:
(1) A practical higher mode generalized force spectrum (HMGFS) model is deduced on the basis of fundamental mode generalized force spectrum (FMGFS) obtained from a wind tunnel and adopting the height-independent fluctuating wind power spectral density and Shiotami-Type spatial coherence function.
(2) Based on the random vibration theory, a practical algebraic formula, in which the higher mode contributions can be included, for evaluating the RMS value of the displacement response is further derived through proper simplification.

References：
[1] H.N. Li, H.F. Bai. High-voltage transmission tower-line system subjected to disaster loads, Progress in Natural Science 2006;16(9):899-911.
[2] J. D. Holmes, Along-wind responses of lattice towers: Part --derivation of expressions for gust response factor, Eng Struct 1994; 16(4):287-92.
[3] J. D. Holmes, Along-wind responses of lattice towers: Part --Aerodynamic damping and deflections, Eng Struct 1996;18(7):483-88.
[4] J.D. Holmes, Along-wind responses of lattice towers: Part--Effective load distributions, Eng Struct 1996; 18(7):489-94.
[5] A.M. Loredo-Souza, A.G Davenport, A novel approach for wind tunnel modelling of transmission lines, J Wind EngInd Aerodyn 2001;89(11-12):1017-29.
[6] A.M. Loredo-Souza, The behavior of transmission lines under high winds, The University of Western Ontario, Ph.D.Thsis, London, Canada,1996.
[7] L.H. Zou. Investigation on model of dynamic wind loads and wind-induced vibration of lattice highrise structures,Ph.D. Thesis, Wuhan University, China, 2006.
[8] X.L.Yu. Wind-induced dynamic responses on lattice towers and simplified evaluation of equivalent wind load, M.D.Thesis, Wuhan University, China, 2006.
[9] American Society of Civil Engineers(ASCE). Wind tunnel studies of buildings and structures, ASCE manuals and reports on engineering practice No. 67, ASCE, New York,
1999.
[10] X.T. Zhang. Wind Engineering of Structure. Beijing:China Architectural Industry Press; 2006.
[11] A. K. Chopra. Dynamics of Structures: Theory and Applications to Earthquake Engineering. 2nd ed.Prentice-Hall, 2000.
[12] X.Z. Chen, A. Kareem, Coupled dynamic analysis and equivalent static wind loads on building with 3-D modes. JStruct Eng, 2005; 131(7):1071-82.
[13] X.Z. Chen., A. Kareem, Dynamic wind effects on buildings with three-dimensional coupled coupled modes.J Eng Mech, 2005; 131(11):1115-25.
[14] X.Z. Chen., A. Kareem, Equivalent static wind loads on low-rise buildings based on full-scale pressure measurements, Eng Struct, 2007;29(10):2563-75.
[15] X.Y. Zhou, M. Gu, Analytical approach considering modal coupling effects for buffeting resonant response of large-span roof structure, Journal of Vibration Engineering, 2006; 9(12):179-183.
[16] A. Kareem, Y. Zhou, Gust loading factor-past, present and future, Gust loading factor-past, present and future, J Wind Eng Ind Aerodyn, 2003;91(12-15):1301-28.