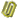Frequency-domain probabilistic solution for MDOF nonlinear system under multi-support seismic excitations作者: Liu-Guohuan,Lian-Jj ,Liang-Chao |
||||||
下载次数:
次 更多论文下载...
PDF(左键浏览,右键另存):
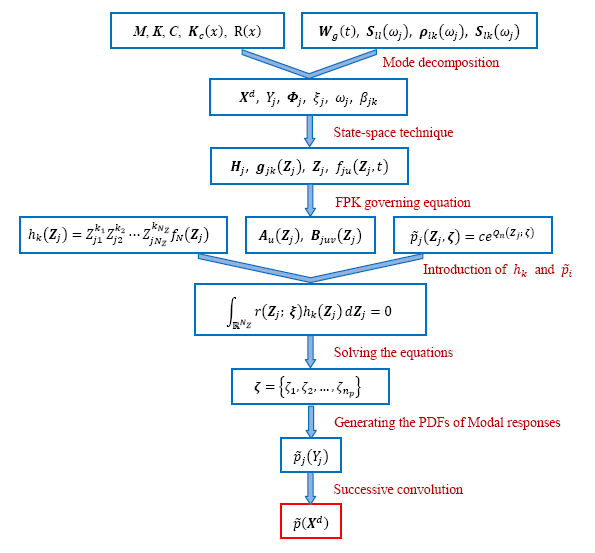
2016,x(xx), Journal of Engineering Mechanics (ASCE)(暂不提供下载) Abstract:As current studies on seismic analysis in frequency domain mainly focus on linear systems, the response spectrum method is inapplicable for the nonlinear system suchas structures equipped with nonlinear base isolations. An effective approach is proposed to investigate probability density functions (PDF) for the responses of nonlinear multi-degree-of-freedom (MDOF) system under multi-support excitations. In this paper, the MDOF system is firstly decoupled by mode decomposition method, andthen the exponential polynomial closure (EPC) method is employed to solve the Fokker-Planck-Kolmogorov (FPK) formulae, which are deduced from the decoupled single-degree-of-freedom (SDOF) equations. In order to consider the multi-support excitations, the coherency spectrums are incorporated into FPK formulae. The advantage of this approach is that the problems in solving MDOF FPK equations are avoided. Moreover, the probabilistic solution is more reasonable and scientific than the peak response calculated by conventional spectrum method. A two-span bridge is taken as an example to calculate the PDF of structural response by Monte Carlo and the proposed methods, and numerical results show that the proposed approach is accurate and efficient. Keywords:Nonlinear stochastic dynamical system; Multi-support excitations; Mode decomposition; Exponential polynomial closure method; Probabilistic solution; Nonlinear elastic support      www.liuguohuan.net 科研团队与课题研究招收与招聘
Introduction: The dynamic response of structures subjected to earthquake ground motion is usually calculated by the direct integral method in time domain and response spectrum method in frequency domain. For simple structures, the direct integral method is widely used and accuracy requirement can also be achieved. However, for complex MDOF systems, the computational time of the direct integral method is remarkably long. Therefore, the response spectrum method is frequently used to estimate the peak value of structural seismic response in engineering practice. In recent years, the response spectrum method is extended to calculate the peak response of the structures with different characteristics such as long-span structure subjected to multi-support seismic excitations (Hao 1989; Kiureghian and Neummhofer 1992; Su et al. 2006; Tian and Li 2010; Tian et al. 2014), non-classically damping system (Foss 1958; Yu and Zhou 2008; Xu 2010; Guo et al. 2011, 2013; Liu et al. 2015) and the structure considering ductility and strain rate effects (Li and Li 2010, 2012; Li et al. 2013). However, for the MDOF system subjected to multi-support excitations, current studies on the dynamic analysis in frequency domain are usually focus on linear structures. Therefore, the response spectrum method is inapplicable for the nonlinear system such as the structure equipped with nonlinear base isolations (Lu et al. 2005; Xu et al. 2009). In the present paper, an effective approach is proposed to investigate PDF for the response of stochastic MDOF system with nonlinear elastic supports under multi-support excitations. It is known that the PDF solution of nonlinear stochastic dynamic system is governed by FPK equation and the exact solution of this equation is very difficult to obtain. Only under some restrictive conditions, the stationary exact solutions are obtainable for some one, two, or few-dimensional system. Therefore, some methods were introduced or extended to obtain the approximate probabilistic solutions of nonlinear stochastic dynamic systems. The most frequently used approximation method is the equivalent linearization or Gaussian closure procedure (Iyengar and Dash 1978). If the structure is highly nonlinear or the multiplicative noise is involved, the probability distribution of the system response is usually far from being Gaussian. In such a case the equivalent linearization and Gaussian closure methods are considered inapplicable. A non-Gaussian closure method (Assaf and Zirkie 1976; Grandall 1980) is proposed using Cram-Charlier series or Hermite polynomial to approximate the PDF solution. This method improves the accuracy of the approximate solution but may lead to negative probability. Stratonovich (1963) proposed the stochastic average method to calculate the PDF solution of response amplitudes of nonlinear systems. This method is merely suitable for the weakly damped systems subjected to weak excitations. Sobczyk and Trebicki (1990) extended the maximum entropy method to the general class of stochastic nonlinear systems and apply it to stochastic nonlinear oscillators. Numerical analysis indicates that the maximum entropy principle can serve as a general method for determining the probability distributions of oscillators. However, it is difficult to extend for MDOF problems.
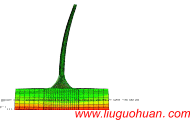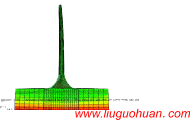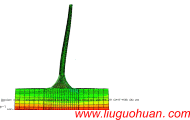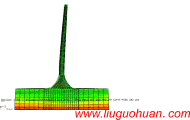
地下多点地震动程序界面
For the seismic analysis of spatial system with underground structure, one may input the multi-point earthquake excitations at the base of the building. In this case, the underground excitation is generated by he seismic wave propagating to the base of the underground structure at a certain depth below the ground.The existing ground PSD, response spectrum and coherence models cannot be directly employed to simulate the multi-support underground motions. Therefore, the underground PSD and underground response spectrum are firstly deduced and then the underground cross-correlation function is further presented. These three theoretical models are firstly employed to establish the total power spectrum matrix and then the underground motions are generated by decomposing the aforementioned matrix using Cholesky decomposition method. Moreover, these three theoretical models are not only necessary conditions to simulate the multi-support earthquake underground motions but also the standards to verify the simulation results. A visual program for simulating multi-support earthquake underground motions is developed and its reliability is verified. Finally, a two-span bridge is taken as an example to calculate its seismic response under both multi-support earthquake ground and underground motions. Numerical results show that the simulation of multi-support earthquake underground motions is significant for both study and engineering application.  
Conclusions:
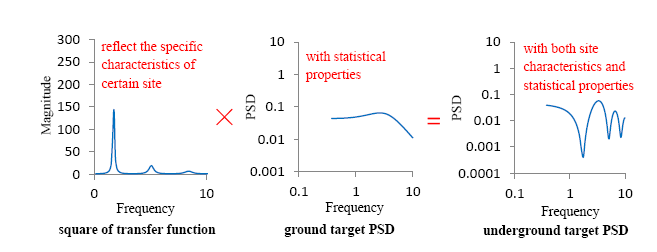
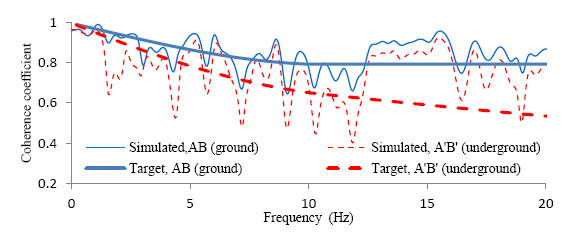
传递函数*地表功率谱=地下目标功率谱 地表(地下)模拟多点地震动功率谱与目标谱对比
www.liuguohuan.net 科研团队与课题研究招收与招聘 |
||||||
| welcome to www.liuguohuan.net |
| 天津大学 建筑工程学院 ; 天津大学 前沿技术研究院; 国家重点实验室-水利工程仿真与安全 |