An efficient approach for seismic analysis of multi-support structures equipped with coupled dampers using spectral moments instead of cross-correlation coefficients作者: Liu-Guohuan,Lian-Jj ,Liang-Chao ,et al |
||||||
下载次数:
次 更多论文下载...
PDF格式(左键浏览,右键另存):
2017,21(5):701-725, Journal of Earthquake Engineering
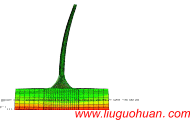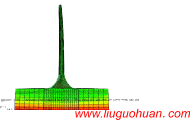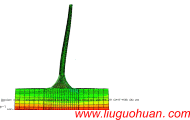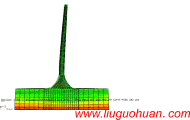
Abstract:A formulation is developed for analyzing the dynamic response of multi-support structures with coupled non-classical damping using spectral moments instead of the frequently used cross-correlation coefficients. Its advantages are that the formulation considering the modal response variances and cross-covariances is more efficient in calculation than the conventional formulation, and the coupled damping of structure is taken into consideration. For the dynamic analysis of a structure equipped with coupled damper, the classical mode decomposition method is inapplicable and the velocity term of the external load in vibration equation cannot be neglected. The dynamic equation is firstly decoupled by complex mode decomposition method in this paper. Then, the complete SRSS rule (c-SRSS) addressed in Heredia-Zavoni’s paper [2011, 2015] is developed to consider the non-classically damping system under multi-support excitations. Moreover, spectral moments of orders higher that 3 are newly introduced into the dynamic analysis and the convergence difficulty for these spectral moments is overcome by employing the band-limited power spectra. A large-span structure equipped with a coupled damper is taken as an example to calculate its dynamic response using the conventional and proposed formulations, and numerical results show that the proposed formulation is accurate and efficient.
Keywords:multi-support earthquake ground motion; seismic response analysis; complex response decomposition method; spectral moments; random vibration; response spectrum method
Introduction: Structural seismic response is usually calculated by direct integration and response spectrum methods. For the structures with a large number of degrees of freedom, the computation efficiency of response spectrum method is much higher than the direct integration method. However, the response spectrum method also has some disadvantages such as the inability to consider nonlinear response and strain rate effect. Due to the high computational efficiency, the response spectrum method is recommended in many seismic design codes and specifications in different countries. Currently researches on response spectrum method mainly focus on extending the application scope and improving the computational efficiency.The multi-support system and non-classically damped system are the hotspots of current research. According to the actual conditions, the earthquake motion is usually characterized by variations in time and space (i.e., the wave passage effect, site coherence effect and local site effect) and the differences in the support motions have an effect on the structural dynamic response, especially for the large span structures. Different kinds of structures, e.g., asymmetric building [Hao and Xiao 1995], multi-storey building [Heredia-Zavoni and Leyva1 2003], spatial-latticed structures [Ye et al. 2011], bridge structures [Bi and Hao 2012; Bao and Hao 2013; Shrestha et al. 2014; Haciefendioglu 2015], embankment dam [Davoodi et al. 2013] and structure-pile-soil system [Kojima et al. 2014], etc., are taken as examples to investigate structural dynamic responses under multi-support seismic excitations. Furthermore, Kiureghian [1981] developed a response spectrum method which is popularly used in frequency domain analysis of structures subjected to multi-support excitations. On the basis of Kiureghian’s work [1981], Su et al. [2006] as well as Ye et al. [2012] improved the computational efficiency of the traditional response spectrum method through detailed theoretical and numerical analysis. Huang et al. [2013] modified the conventional response spectrum method to make it more precise and convenient for engineering applications. Moreover, the seismic analysis for the non-classically damped linear systems has drawn a lot of attention because it is noticed that there are many structures whose damping are non-uniform, e.g., structures composed of different materials with different damping and structures equipped with supplemental dampers. The mode decomposition method for the multi-degree-of-freedom (MDOF) dynamic equation with non-orthogonal damping matrix is studied by many researchers. Foss [1958] proposed a method to calculate the estimation of damping matrices of cable-stayed bridges by known damping ratios. According to the works of Velesos and Ventura [1986] as well as Greco and Santini [2002], some techniques for the dynamic analysis of non-classically damped linear system is reviewed and compared. Xu et al. [2004] proposed a method to calculate the stationary random response of a non-classically damped structure and the physical meanings of the parameters involved in the formulae are clearly clarified. Zhou el al. [2004] presented a complex response spectrum method for the non-classically damping system and the calculation involved in the conventional method is considerably simplified. Then, Yu and Zhou [2008] extended the complex response spectrum method to the multi-support structure. Moreover, the dynamic responses of structures equipped with different kinds of coupled dampers, e.g. viscoelastic and magnetorheological dampers, are analyzed by Xu et al. [2003, 2007, 2012]. In the present paper, we further investigate the dynamic response for the multi-support system equipped with a coupled damper.Many efforts have been devoted to improve the formulation of the mode combination rule to make the calculation more efficient and convenient. Rosenblueth [1951] presented a widely used combination rule named Square Root of the Sum of Squares (SRSS). It has a simple computation formula, which neglect the cross-covariance between modal responses. Generally speaking, SRSS combination rule works well when the modal frequencies are well-separated. However, the contribution to total response from cross-covariance between modal responses becomes more significant for the system with closely spaced modal frequencies [Heredia-Zavoni, 2011]. In such a case, SRSS combination rule has a poor accuracy. Kiureghian [1980] proposed the Complete Quadratic Combination (CQC) rule, in which simple expressions for the correlation coefficients between modal responses are given. For the wide-banded excitation, this approximation works well. However, for narrow bandwidth seismic inputs it may not estimate the structural response accurately. Heredia-Zavoni [2011; 2015] presented the complete SRSS rule (c-SRSS), which is developed from the conventional SRSS method. In the c-SRSS rule the spectral moments of the structural response are expressed rigorously in terms of the spectral moments of uncoupled modal responses and of some coefficients that can be computed straightforwardly as a function of modal frequencies and damping, without involving the computation of cross-correlation coefficients between modal responses. Thus, the accuracy of c-SRSS method is higher than that of SRSS method, especially for the system with closely spaced modal frequencies. The c-SRSS formulation provides an efficient and promising way to calculate the modal response cross-covariances.In this paper, the formulation to calculate the structural dynamic response is extended and improved for multi-support structures equipped with coupled dampers. Especially for the system with closely spaced modal frequencies, the modal response variances and cross-covariances can be efficiently calculated using the spectral moments. The complex mode decomposition method is adopted to decouple the dynamic equation for the coupled damping structure due to the non-orthogonal damping matrix. Based on the uncoupled mode responses, the c-SRSS mode combination rule is employed to calculate the total response. Moreover, the spectral moments of uncoupled modal responses are defined (Section 3.2), and the structural response is expressed by the combination of the aforementioned spectral moments and coefficients that are functions of modal frequencies and damping. In such a case the structural response considering modal response variances and cross-covariances can be calculated without involving the cross-correlation coefficients between modal responses. The velocity term of the external load in dynamic equation, which is negligible for the classically damped system, cannot be neglected for the structure equipped with a coupled damper. Therefore, the spectral moments with higher and lower orders than that for the classically damped system are involved in the calculation. It is noted that the spectral moment is expressed as an integration of polynomial function of frequency, and the integral interval ranges from 0 to infinity. According to integral principle, the convergence of the spectral moment is directly affected by its order. The dynamic excitations with band-limited power spectra are adopted to guarantee the convergence of spectral moments. The advantage of the proposed formulation is that the cross-correlation coefficients related to structural response do not appear so that the computational efforts are significantly reduced, especially for the system with large number of degrees of freedom. Furthermore, an example is given in Section 4 to indicate the accuracy and efficiency of the formulation.
  In this paper, the formulation estimating the maximum structural response using spectral moments instead of cross-correlation coefficients is extended to the multi-support system with coupled non-classical damping. Main works are summarized as follows: For the multi-support system equipped with a coupled damper, the dynamic equation is firstly decoupled by complex mode decomposition method. Then, the c-SRSS method is developed and the spectral moments is adopted to calculate the cross-correlation term of modal responses under multi-support seismic excitations. The spectral moments of orders higher than 3 are newly introduced into the dynamic analysis, due to the innegligible velocity term in external load of the dynamic equation. Moreover, the band-limited spectra are adopted to overcome the convergence difficulty of these spectral moments. The advantages of the proposed approach are that the formulation considering modal response variances and cross-covariances is efficient in calculation, and the coupled damping of structure is taken into consideration. The dynamic response of the numerical example is calculated by the conventional and proposed formulations, respectively, and the results indicate that the proposed formulation is accurate and efficient. The c-SRSS formulation provides an efficient and promising way to calculate the modal response cross-covariances. The further researches may focus on how to consider the material and geometrical nonlinearities and strain rate effects on the basis of c-SRSS method. |
||||||
| welcome to www.liuguohuan.net |
| 天津大学 建筑工程学院 ; 天津大学 前沿技术研究院; 国家重点实验室-水利工程仿真与安全 |