An effective approach for simulating multi-support earthquake underground motions作者: Liu-Guohuan,Jijian Lian,Chao Liang,Mi Zhao |
||||||
下载次数:
次 更多论文下载...
PDF(左键浏览,右键另存):
Abstract:An effective approach to simulate the multi-support earthquake underground motions iscproposed in this paper and the key factor for this approach (i.e. underground crosscorrelation function) is presented in advance. Previous studies are mainly focused on the multi-support ground motions due to the absence of the necessary conditions to simulate underground motions, i.e., underground power spectral density (PSD), underground response spectrum and, especially, underground cross-correlation function. In this paper, the underground PSD and response spectrum are firstly derived and the cross-correlation function between the underground motions at positions with different horizontal and vertical coordinates is further deduced. The physical meanings of the parameters in this approach are explicitly clarified. Moreover, a visual program for generating the multi-support earthquake underground motions is developed and the reliability of the generated motions is verified. Finally, a two-span bridge is taken as an example to investigate structural responses under multi-support earthquake underground excitations. Numerical results show that the dynamic responses under multi-support earthquake underground motions are significantly different from those under multi-support earthquake ground motions. Results indicate that the simulation of multi-support earthquake underground motions is significant for both study and engineering application. Introduction: Dynamic responses of structures under earthquake excitations are related to and even dependent upon the seismic motion inputs, especially for a large-span structure subjected to multi-support seismic excitations. According to the actual conditions, the earthquake motion is usually characterized by variations in time and space (i.e., the wave passage effect, site coherence effect and local site effect) and the differences in the support motions have a significant influence on the structural internal forces (Hao 1989; Berrah and Kausel 1992). Many theoretical models (especially the coherency function models) are proposed to simulate the spatially varying ground motions. Ta et al. (2010) generalized the Soize’s model (2006) toaccount independently for the anisotropy index and the fluctuation level, which leads to major differences n the wave propagation regimes and is beneficial to build the predictive models of the dynamic behavior of inhomogenous and complex structures. Bi and Hao (2011, 2012) firstly investigated the influences of Layered irregular sites and random soil properties on coherency functions and then presented an approximate method to model and simulate spatially varying ground motions on the surface of an uneven site with non-uniform conditions at different locations. Liu et al. (2012) proposed a method for generating multi-point earthquake motions on the basis of focal mechanism. Zentner and Poirion (2012) introduced anew method for generating synthetic ground motion, based on Karhunen-Loève decomposition and a non-Gaussian stochastic model. The proposed method enables the structural analyst to simulate ground motion time histories featuring the properties such as peak ground acceleration (PGA), cumulative absolute velocity and Arias intensity. Su and Shi (2013) proposed a displacement-based earthquake loss assessment methodology for RC frames when the influence of masonry infill panels is taken into account. However, above studies are mainly focused on earthquake ground motions and the multi-support earthquake underground motions are rarely reported in the published literatures. Different kinds of structures (e.g., single span bridges, train-bridge system and spatial-reticulated structures, etc.) are taken as examples to investigate structural dynamic responses under multi-support seismic excitations, which are generated by the conventional approach (Alexander 2008; Tian and Yang 2009; Xu 2010; Zhang et al. 2010; Ye et al. 2011; Tian and Li 2012; Guo et al. 2013; Tian et al. 2014; Shrestha et al. 2014). A new methodology is set up and implemented into a computer code by Sextos et al. (2003) for deriving sets of appropriately modified time histories and spring–dashpot coefficients at eachsupport of a bridge with account for spatial variability, local site conditions and soil–foundation–superstructure interaction, for the purposes of inelastic dynamic analysis of RC bridges. Several investigators (Berrah and Kausel 1992; Kiureghian and Neummhofer 1992; Su et al. 2006; Yu and Zhou32008) extended the response spectrum method for the case of spatially varying ground excitations to estimate the peak structural response. It is noted that for the large-span spatial structure system with underground structure, regarding ground motions as underground input is unreasonable. According to Zerva’s productive work (2009), the seismic ground deformations are selected as the seismic loads for the underground structures (e.g. buried pipelines and tunnels). However, there continues to be a lack of effective theoretical approaches to simulate the multi-support underground earthquake motions (e.g. acceleration, velocity and displacement time histories).
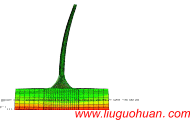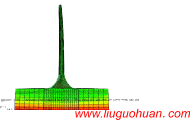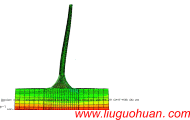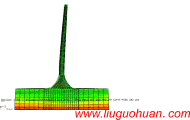
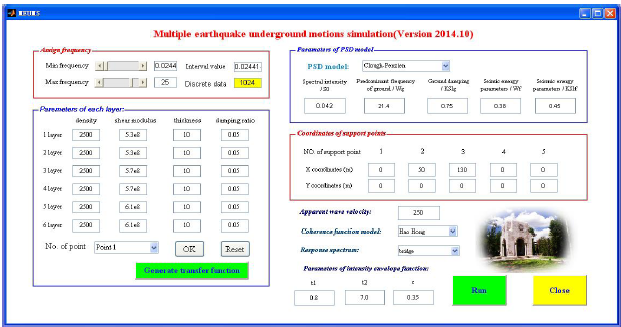
地下多点地震动程序界面
For the seismic analysis of spatial system with underground structure, one may input the multi-point earthquake excitations at the base of the building. In this case, the underground excitation is generated by he seismic wave propagating to the base of the underground structure at a certain depth below the ground.The existing ground PSD, response spectrum and coherence models cannot be directly employed to simulate the multi-support underground motions. Therefore, the underground PSD and underground response spectrum are firstly deduced and then the underground cross-correlation function is further presented. These three theoretical models are firstly employed to establish the total power spectrum matrix and then the underground motions are generated by decomposing the aforementioned matrix using Cholesky decomposition method. Moreover, these three theoretical models are not only necessary conditions to simulate the multi-support earthquake underground motions but also the standards to verify the simulation results. A visual program for simulating multi-support earthquake underground motions is developed and its reliability is verified. Finally, a two-span bridge is taken as an example to calculate its seismic response under both multi-support earthquake ground and underground motions. Numerical results show that the simulation of multi-support earthquake underground motions is significant for both study and engineering application.  
Conclusions:
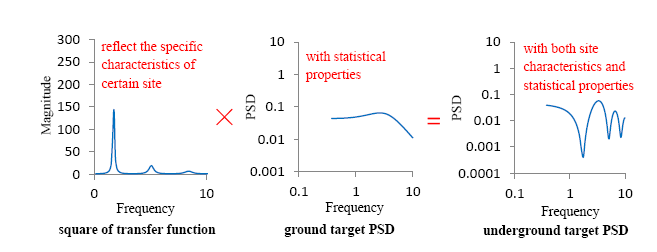
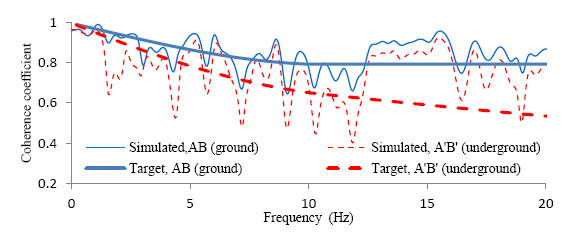
传递函数*地表功率谱=地下目标功率谱 地表(地下)模拟多点地震动功率谱与目标谱对比
www.liuguohuan.net 科研团队与课题研究招收与招聘 |
||||||
| welcome to www.liuguohuan.net |
| 天津大学 建筑工程学院 ; 天津大学 前沿技术研究院; 国家重点实验室-水利工程仿真与安全 |