PDF格式（左键浏览，右键另存）：

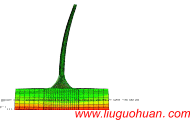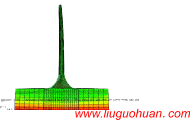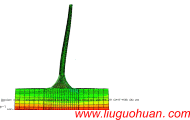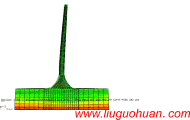
Possible existing seismic analysis errors of long span structures and bridges while utilizing multi-point earthquake calculation models

(2013)《Bulletin of Earthquake Engineering》

Abstract：A long-span structure is a common type of public building, but its seismic characteristics are distinct from other types of buildings because of its long span. Calculation models considering multi-point excitation are required in the seismic analysis of long-span structures. However, correlative studies have already clearly shown that important but often overlooked errors exist in previously developed multi-point excitation calculation models. The process of establishing displacement and acceleration models for multi-point seismic analysis is reviewed. Error sources and criteria of the two models are explained using rigorous theoretical derivation. Error characteristics and distributions in multiple structural types, such as ordinary structures without dampers and damper-installed structures with concentrated damping, are also described. Modifications for multi-point excitation displacement and acceleration models, for time history and stochastic analysis, respectively, are proposed, and these modified models are used to assess errors in the conventional models. Numerical examples are solved using conventional displacement and acceleration models and two corresponding modified models. The properties, components and distribution of errors in the conventional models are demonstrated. The findings presented in this paper can provide a sound basis for the practical application of multi-point excitation calculation models in seismic analysis.
Keywords：Long-span structure · Seismic analysis · Multi-point excitation ·Calculation model · Damping problem

Introduction
Social progress and economic development in recent years have stimulated the growth of the public-sector construction industry around the world and especially in China. Numerous buildings with complex structural styles have been constructed in China, such as the “Bird’s Nest” National Stadium, the World Expo Theme Pavilion in Shanghai, high-speed railway stations and others. All of these large structures possess long-span characteristics and often are landmarks of a city. Long-span structures play a role in transportation structures. Urbanization and urban population growth have increased transportation demand and vehicle traffic.Alarge number of interurban elevated bridges are to be constructed to meet these needs. High-speed railway lines, a large proportion of which are often bridges, are being built as well. Because of their important functions and symbolic significance, seismic analysis and design of longspan structures and bridges have attracted widespread attention from scholars. The seismic response characteristics of long-span structures are clearly distinct from ordinary structures, especially when the structural span’s wavelength and the ground’s wavelength are the same order of magnitude. Differences between multiple earthquake excitations applied to supports should be considered, mainly in connection with the following three important factors: wave passage effects, local site effects and site coherence effects. In general, calculated results ignoring multi-point excitation characteristics cannot accurately describe actual structural response.
Seismic analysis of long-span structures under multi-point excitation has become a focus of current research. Two calculationmodels are usually adopted, the displacementmodel and the acceleration model. The displacement model takes the displacement of the ground in an earthquake as its input and uses the absolute structural displacement as a key parameter. This model has a wide range of application and is suitable for both linear and nonlinear analysis. Using the displacement model, Yamamura and Tanaka (1990), Hao (1991), Hao and Xiao (1995), Su et al. (2006) have carried out a great deal of numericalwork on time history analysis of engineering structures. The acceleration model takes the acceleration of the ground in an earthquake as its input. This model was first proposed by Clough and Penzien (1975) based on rigorous theoretical derivation. It is similar in form to the model that is established under uniform seismic excitation. The acceleration model has good accuracy but is only suitable for linear analysis because of the superposition principle adopted in its derivation. However, this point is often overlooked in application, and applying the accelerationmodel to nonlinear analysis of long-span structures leads to incorrect results and unreasonable designs. Acceleration response spectrummethods suitable for seismic analysis of long-span structures have been derived by Kiureghian andAnsgar (1992) andBerrah and Kausel (1993). Given that both the displacement model and the acceleration model have certain inherent assumptions associated with them, they possess some theoretical defects and are not applicable for all conditions. Considering that few scholars have studied the error-inducing aspects of these models,we identified problem of the displacementmodel in ordinary structures with Rayleigh damping and showed that the problem can be addressed by the use of a massless rigid element (MRE) in the SAP2000 software (Liu et al. 2010). However, in the previous study, only ordinary structures with Rayleigh damping were considered. As the styles of longspan structures are usually diverse and conventional designs cannot satisfy practical  eismic
needs, control techniques, such as isolation, dampers and so on, are often introduced in design. Therefore, long-span structures with isolation or dampers that possess  concentrated damping characteristics appear frequently in engineering. Considering that the reliability and error potential of conventional seismic calculation models have not been addressed before, the study described in this paper is considered valuable and timely.
Based on research previously conducted by we, two calculation models (the displacement model and the acceleration model) for seismic analysis of long-span structures subjected to multi-point excitation are systematically studied, focusing in particular on their applicability and error potential for ordinary structures and damper-installed structures that possess concentrated damping characteristics. First, sources of error and situations in which they may arise are analyzed for the two models by rigorous theoretical derivation. It is demonstrated that the error problem is mainly the result of a non-proportional damping distribution. Second, modifications to the displacement and acceleration models, for time history and stochastic analysis, respectively, are presented. Third, numerical analyses are presented to demonstrate the errormagnitudes and distributions of the two models for different types of structures. The effectiveness of the proposed model modifications is also verified. The results of the study described in this paper provide important guidance for the rational use and modification of calculation models for seismic analysis of long-span structures under multi-point excitation in earthquakes.

Conclusions
This paper presents a systematic study of calculation models for seismic analysis of longspan structures under multi-point excitation in an earthquake. Several calculation models are derived based on dynamic theory, and then an important but often overlooked problem in conventional calculationmodels is identified and described. Sources of error and situations in which theymay occur with the displacementmodel and the accelerationmodel are explained, and model modifications for time history and stochastic analysis are presented. Based on the theoretical derivations and numerical analyses presented in this paper, the following conclusions are drawn:
(1) The displacementmodel and the accelerationmodel have different ranges of applicability in seismic analysis of long-span structures. The displacement model is  applicable for both linear and nonlinear analysis, but the acceleration model can only used in linear cases because of the adoption of the superposition principle in its derivation. The errors of the two models are both produced by ignoring the damping terms, such that the error problem is actually a damping problem. It should be noted that the two models have different damping assumptions and error-induced mechanisms.
(2) For an ordinary structure with Rayleigh damping, the displacement model is sufficiently accurate for calculation of the seismic response structure, except when the bottom elements are too finely divided. Obvious errors occurmainly in the calculated displacements of bottom elements and are affected by elemental division. For structures with dampers at the bottom, both damping coefficients provided by dampers and the ratio of ground velocity to acceleration (PGV/PGA) have an important influence on the magnitude of error associated with the displacementmodel, so that in a near-fault earthquake, the error is more obvious. Unlike the case with an ordinary structure, errors occur for both thebottom and internal parts of long-span structure. Increases in the damping coefficient correspond to increasingly obvious errors for bottom elements, while errors for internal elements tend to remain stable.
(3) In an ordinary structure with Rayleigh damping, the acceleration model has good calculation precision and is not influenced by bottom elemental division, so it can be considered an accurate method of seismic analysis for this type of structure. When dampers are installed in the structure, regardless of whether concentrated damping exists at the bottom or within internal parts of the structure, the calculation precision of the acceleration model will be affected, and some error will result.
(4) When concentrated damping exists at the supports, the responses of all structural nodes calculated with the acceleration model exhibit obvious error. As with the  displacement model, the error of the accelerationmodel ismainly a function of the damping coefficients and the ratio of ground velocity to acceleration (PGV/PGA), so there is obvious error in the calculated accelerations in the case of a near-fault earthquake. Increases in the damping coefficient correspond to increasingly obvious errors for bottom elements, while errors for internal elements tend to remain stable.
(5) When concentrated damping exists within the internal parts of the structure, the error produced by the acceleration model for bottom elements is relatively small, and some
error is also produced for the internal parts. Similarly, the error produced by the acceleration model is affected by the damping coefficient and the ratio of ground velocity to
acceleration (PGV/PGA), so there is obvious error in the calculated accelerations in the case of a near-fault earthquake. Errors produced by the acceleration model are closely
related to the damper configurations and the different motions of multiple supports in an earthquake. Increases in the damping coefficient correspond to increasingly obvious
errors for the bottom elements, while errors for internal elements tend to remain stable.Differences in the motion of all of the supports in an earthquake affect the error associated with the acceleration model, and while the differences tend to be distinct, the errors tend to be obvious. If there are no differences in the motion of the supports, the error produced by the acceleration model is too small to be neglected.
(6) The modification to the time history analysis method described in this paper based on fundamental dynamic theory and yields results equal in accuracy to those obtained by the large mass method or the large stiffness method. Moreover, based on the pseudoexcitation method, stochastic expressions are derived and improved to conduct efficient and accurate calculations.Given that the pseudo-excitationmethod utilizes random excitation as a sinusoidal input, the calculation error associated with stochastic analysis is similar in magnitude to that associated with time history analysis.

References：
[1] BerrahM, Kausel E (1993) Amodal combination rule for spatially varying seismicmotions. Earthq Eng Struct Dyn 22(9):791–800
[2] Clough RW, Penzien J (1975) Dynamics of structures. McGraw-Hill Book Co, New York
[3] Hao H (1991) Response of multiply-supported rigid plate to spatially correlated seismic excitations. Earthq Eng Struct Dyn 20(9):821–838
[4] Hao H, Xiao ND (1995) Response of asymmetric structures to multiple ground motions. J Struct Eng 121(11):1557–1564
[5] Kiureghian AD, Ansgar N (1992) Response spectrum method for multi-support seismic excitations. Earthq Eng Struct Dyn 21(8):713–740
[6] Lin JH(1992)AfastCQCalgorithm of PSD matrices for random seismic responses.Comput Struct 44(3):683–687
[7] Liu GH, GuoW, Li HN (2010) An effective and practical method for solving an unnegligible problem inherent in the current calculation model for multi-support seismic analysis of structures. Sci China (Technological Sciences) 53(7):1774–1784
[8] Su L, Dong SL, Kato S (2006) A new average response spectrum method for linear response analysis of structures to spatial earthquake ground motions. Eng Struct 28(13):1835–1842
[9] Wilson EL (2004) Static and dynamic analysis of structures: a physical approach with emphasis on earthquake engineering. Computer and structures, Inc., Berkley
[10] Yamamura N, Tanaka H (1990) Response analysis of flexible MDF systems for multiple-support seismic excitation. Earthq Eng Struct Dyn 19(3):345–357