PDF格式（左键浏览，右键另存）：

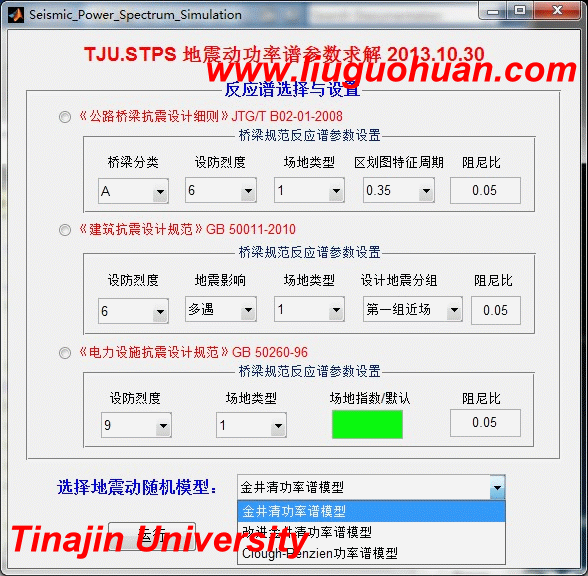
A fast stochastic analysis method for soil-structure interaction system

Vol.13 《Electronic Journal of Geotechnical Engineering》

Abstract：In this paper, a fast stochastic analysis method is presented to compute the seismic response of the soil-structure interaction system. Using the classical modal decomposition and the pseudo-force method, a closed form sequence is developed for iterative computation. It can account for the non-proportional damping and dynamic interaction between the soil region and the structure. Moreover, the pseudo-excitation method is introduced in the derivation for improving the computational efficiency of the stochastic analysis. The necessary and sufficient condition for convergence of the sequence is also provided. Compared with the forced decoupling method, the proposed method can significantly improve the accuracy of the results without obviously increasing computational efforts. In the end, some numerical examples are carried out to examine the accuracy and convergence of the new method.
Keywords：soil-structure interaction system; stochastic analysis; iterative method.

Introduction
Soil-structure interaction is a collection of phenomena in the response of structures caused by the flexibility of the foundation soils, as well as in the response of soil region caused by the presence of structures. During the last three decades, many studies on the subject have been carried out (Seed, et al., 1975; Veletsos and Prasad, 1989; Zhang, et al.,1999; Lou and Wu, 1999; Ghiocel and Ghanem, 2002; Gao, et al., 2009). Because the soil-structure interaction system consists of two parts with distinct damping
characteristics, which is usually called non-proportional damping, the equations of motion can not be represented by assembly of a series of independent oscillators. As the most common approach, the forced decoupling method (Elishakaff and Lyon, 1986) is adopted for seismic analysis of non-proportionally damped system by simply  eglecting
the off-diagonal elements of the transformed damping matrix, which is appealing to the design professionals because it enable the use of the traditional modal analysis methods.When the damping characteristic of the combined system is approximately identical, the error introduced by the method is so small that it can usually be ignored. However, the results obtained by this method are not exactly accurate theoretically and might introduce significant error in some cases, especially for the soil-structure interaction system, the two parts of which possess dramatically distinct properties. Therefore, in order to obtain more exact results, the complex eigenproperties via state-space approach (Foss, 1958) is developed for the modal analysis. However, the calculation of complex eigenvalues problem is cumbersome and time-consuming, and thus attempts to overcome the computational difficulties of this approach have been carried out (Lou, et al., 2003; Karen and Mohsen, 2005; Fernando and María, 2006; Hea, et al., 2007). On the other hand, based on the pseudo force method (Claret and Venancio, 1991; Lin, et al., 2003), an iterative procedure for computing the transfer function matrix of a non-classically damped system has also been developed (Jandid and Datta, 1993; Zavoni, et al., 2006).The iterative methods have more advantages than the complex modal superposition methods in terms of speed, and it retains the advantages of the real-valued modal superposition methods. Therefore, the iterative method is generally considered to be more applicable than the other methods either for time history or stochastic analysis of combined system with distinct damping characteristics.
In this paper, a fast iterative method is proposed for the stochastic analysis of soilstructure interaction system. It can account for the non-proportional damping by introducing the pseudo-force method and, at the same time, the pseudo-excitation method is adopted for improving the computational efficiency. Besides, the classical modal decomposition, which is more applicable in the practical engineering, is used in the new method instead of the complex or real mode shapes of the combined system. Finally two model of soil-structure system are taken as numerical examples to illustrate the proposed method.

Conclusions
In this paper, a fast stochastic analysis method of soil-structure interaction system has been presented. In the new method, the pseudo-excitation method and the classical
modal decomposition is adopted to derivate an iterative sequence, which can exactly account for the non-proportional damping and dynamic interaction between the soil
region and the structure without obviously increasing computational effort. Furthermore,the new method’s accuracy and convergence have been proved by some numerical
examples belonging to two different models of soil-structure interaction system.

References：
[1] Seed, H.B., Hwang, R.N., Lysmer, J. (1975) “Soil-Structure Interaction Analyses for Seismic Response,” Journal of the Geotechnical Engineering Division, 101(5): 439-457.
[2] Veletsos, A.S., Prasad, A.M. (1989) “Seismic interaction of structures and soils:stochastic approach,” Journal of Structural Engineering, 115(4): 935-956.
[3] Zhang, X., Wegner, J.L., Haddow, J.B. (1999) “Three-dimensional dynamic soilstructure interaction analysis in the time domain,” Earthquake Engineering and Structural Dynamics, 28(12): 1501-1524.
[4] Lou, M.L., Wu, J.N. (1999) “Seismic response analysis of pile foundation structure system,” China Civil Engineering Journal, 32(5): 56-61. (in Chinese)
[5] Ghiocel, D.M., Ghanem, R.G. (2002) “Stochastic finite-element analysis of seismic soil-structure interaction,” Journal of Engineering Mechanics, 128(1): 66-77.
[6] Gao, Q., Lin, J.H., Zhong, W.X., Howson, W.P., and Williams, F.W. (2009)“Isotropic layered soil–structure interaction caused by stationary random excitations,” International Journal of Solids and Structures, 46(3-4): 455-463.
[7] Elishakaff, I., Lyon, H.R. (1986) “Random vibration-status recent developments,”Elsevier Science Publishers, New York.
[8] Foss, K.A. (1958) “Coordinates which uncouple the equation of motion of damped linear dynamic systems,” Journal of Applied Mechanics, 25(1): 361-364.
[9] Lou, M.L., Duan, Q., Chen, G.D. (2003) “Modal perturbation method and its applications in structural systems,” Journal of Engineering Mechanics, 169(8): 935-943.
[10] Karen, K., Mohsen, G.A. (2005) “New approaches for non-classically damped system eigenanalysis,” Earthquake Engineering and Structural Dynamics, 34(9): 1073-1087.
[11] Fernando, C., María, J.E. (2006) “Computational methods for complex eigenproblem in finite element analysis of structural systems with viscoelastic damping treatments,”
Computer Methods in Applied Mechanics and Engineering, 195(44-47): 6448-6462.
[12] Hea, J.J., Jianga, J.S., B. Xu, B., (2007) “Modal reanalysis methods for structural large topological modifications with added degrees of freedom and non-classical damping,” Finite Elements in Analysis and Design, 44(1-2): 75-85.
[13] Claret, A.M., Venancio, F.F. (1991) “A modal superposition pseudo-force method for dynamic analysis of structural systems with non-proportional damping,” Earthquake
Engineering and Structural Dynamics, 20(4): 303-315.
[14] Lin, F.B., Wang, Y.K., Cho, Y.S. (2003) “A pseudo-force iterative method with separate scale factors for dynamic analysis of structures with non-proportional damping,” Earthquake Engineering and Structural Dynamics, 32(2): 329-337.
[15] Jandid, R.S., Datta, T.K. (1993) “Spectral analysis of systems with non-classical damping using classical mode superposition technique,” Earthquake Engineering and
Structural Dynamics, 22(8): 723-735.
[16] Zavoni, E.H., Pérez, A.P., and Cicilia, F.B. (2006) “A method for the transfer function matrix of combined primary-secondary systems using classical modal decomposition,” Earthquake Engineering and Structural Dynamics, 35(2): 251-266.
[17] Lou, M.L., Zhao, Y.L. (1994) “The substructure method for dam-foundation dynamic interaction analysis,” Journal of Vibration Engineering, 7(2): 161-166. (in Chinese)
[18] Jin, F., Zhang, C.H., Wang G.L. (1997) “A time domain model of arch dam-rock foundation interaction,” China Civil Engineering Journal, 30(1): 43-51. (in Chinese)
[19] Bi, J.H., Zhang, H. (2003) “Anti-seismic study on metrotunnel based on coupling numerical analysis method,” Rock and Soil Mechanics, 24(5): 800-803. (in Chinese)
[20] Li, J.B., Chen, J.Y., Lin, G. (2004) “Finite element damping-extraction method for dynamic interaction time domain analysis of non-homogeneous unbounded rock” Chinese Journal of Geotechnical Engineering, 26(2): 263-267.
[21] Lin, J.H. (1992) “A fast CQC algorithm of PSD matrices for random seismic responses,” Computers and Structures, 44(3): 683-687.
[22] Xu, Y.L., Zhang, W.S. (2001) “Modal analysis and seismic response of steel Frames with Connection Dampers,” Engineering Structures, 23(4): 385-396.
[23] Lin, J.H., Zhang, Y.H. (2005) “Vibration and Shock Handbook, Chapter 30: Seismic Random Vibration of Long-span Structures,” CRC Press: Boca Raton, FL.
[24] Igusa, T., Kiureghian, D.A., Sackman, J. (1984) “Modal decomposition method for stationary response of non-classically damped systems,” Earthquake Engineering and
Structural Dynamics, 12(1):121-136.
[25] Jangid, R.S., Datta, T.K. (1993) “Spectral analysis of systems with non-classical damping using classical mode superposition technique,” Earthquake Engineering and
Structural Dynamics, 22(8):723-735.
[26] Wolf, J.P., Somaini, D.R. (1983) “Approximate dynamic model of embedded foundation in time domain,” Earthquake Engineering and Structural Dynamics, 14(5): 683-703.
[27] De Barros, F.C.P., Luco, J.E. (1990) “Discrete models for vertical vibrations of surface and embedded foundation,” Earthquake Engineering and Structural Dynamics,19(2): 289-303.
[28] Jean, W.Y., Lin, T.W., Penzien, J. (1990) “System parameter of soil foundation for time domain dynamic analysis,” Earthquake Engineering and Structural Dynamics, 19(4): 541-553.
[29] Ruan, M.T., Lin, G. (1996) “2-DOF lumped-parameter model of dynamic impedances of foundation soils,” Journal of Dalian University of Technology, 36(4):477-482. (in  Chinese)
[30] Wang, M.S., Pan, G.D., Zhou, X.Y. (2007) “Soil-structure interaction analysis based on the soil lumped parameters model,” Journal of University of Science and Technology Beijing, 29(1): 5-10. (in Chinese)